Trade Logic

Background: Prediction markets

Trade Logic has been kicking around in my head since I learned about Robin Hanson's idea of prediction markets¹ around 1991.

A prediction market is a way of aggregating good-faith information about an issue. It's basically:

• define some issue whose answer isn't know yet but will be,
• take bets on it
• later when the answer is known, pay off just the bets that were right.

In prediction markets, the bets always occur in opposing pairs, which I call yes and no. I'll illustrate it like this:

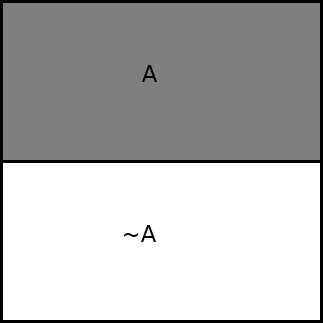
In these diagrams, the entire square represents one monetary unit. It's as if the diagram represented a way to partition $1. Not into smaller amounts of money, but into parts called yes and no, which together always add up to $1.

Introducing Trade Logic

As I talked about earlier, I want to add logic operations to prediction markets for certain reasons.

I've already hinted at one piece of the puzzle: each issue represents a separate way to decompose $1. Furthermore, pieces that are the same part of the same decomposition are interchangeable.

In Trade Logic, each issue (each decomposition) also corresponds to a formula. So when I write a or b in the following discussion, it refers to an issue in a prediction market, as well as to a formula and to a way of decomposing $1.

Trade Logic works by assembling the conclusion from parts of the premise(s). There may be parts left over. That is, bettors can buy yes or no of one or more issues and then assemble those pieces in a different way to form another issue.

That's how the logic itself works, but we also have to ask about incentives. Why would traders want to do that? They would if the new issue is trading at a too-high price, to make a profit by arbitrage. As a rule, that sort of situation is deterred and if it does arise it is quickly corrected. So as a consequence of the Efficient Market Assumption, Trade Logic reasons about related issues.

The unary operator not

The unary operator not, in a formula, is equivalent to swapping the sides of the issue. It swaps a yes for a no and vice versa. So a yes of a is the same as a no of ~a.

Basic binary operators to combine issues

Overview

Beyond this, we can combine two issues into a third issue. That's equivalent to combining their formulas under a binary operator. To do so, we must define a corresponding decomposition.

I'll call the issues being combined a and b.

This is composed of the a diagram above and a b diagram, which is just about the same and the a diagram except I have drawn it at right angles to a.

and

The and operator combines a and b into a new issue, a & b. A yes share of a & b pays off exactly when both a and b would pay off yes. A no share of a & b pays off when either a or b is judged no.

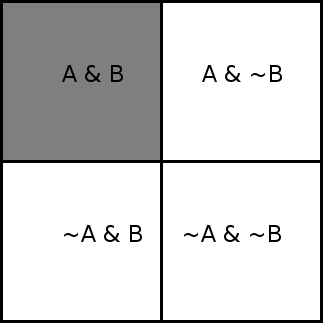
Nothing much changes if one of the issues is finalized before the other. A finalized issue just has a fixed value for yes and no payoffs; usually one is worth 1.0 and the other is worth 0.0.

So if, say, b yes was judged true, it's as if the ~b column of the diagram was eliminated and the b column was stretched to cover the entire square.

or

Similarly, the or operator combines a and b into a new issue, a V b, which pays off yes when either a or b pay off yes.

if

We're interpreting if as material implication, so

a -> b

means the same as

~a V b

So a -> b is just:

Definitions and variables

Motivation

To use formulas in a practical way, we'd like to be able to define abbreviations for subformulas that are used frequently. For abbreviations to do the job, they need to be parameterized and the parameters need to be sharable. So we need some sort of definitions and variables.

Variables are instantiatable

We need the issues to be bettable. The motivation is not so much to make them decidable, it is to give appropriate values to issues that turn out to be fuzzily true.

Consider an issue that has always held true (yes trades at nearly $1.0), until a single exception to the rule is found. Should that issue now trade at $0? No. That would make traders afraid to touch any universal rule, which might collapse to $0 at any time. But if it's trading at a high price and is treated as universally quantified, bettors can cheaply "prove" that the exception is false, though it's true. This situation is a money pump.

To avoid that dilemma, the rule is that all variables are ultimately instantiatable by operations that select examples, rather than being universally quantified or existentially quantified. That doesn't mean that issues have specific examples associated with them; they don't. It means that there is a set way for finding an example that doesn't rely on somebody hand-picking one.

A selection operation would generally mean drawing a random element from a given distribution. A distribution can be just a single example; then it's just a literal. There will be rules about how random number generation should be done, and how many examples to select, and how to settle (or partly settle) an issue for a given number of examples. I won't expand on the various rules right now. That's Crypto and Information Economy and Statistics.

They are instantiatable transitively

I said variables are "ultimately" instantiatable. That means that a given variable might not directly be instantiatable by a selection operation, but it's connected to something that is, or to something that's connected to something (etc).

The treatment here is largely borrowed from Mercury and Prolog.

Predicates have modes. A mode maps each parameter in an argument list to either in or out. A predicate is applied in one of its modes.

For every legal mode of a formula, there must exist an ordering of predicate applications where:

• At the beginning, every variable is free. It will transition to bound at some point. (If it doesn't, that just means it's irrelevant)
• For each predicate application:
  • A legal mode for that predicate is used.
  • For every parameter that has instantiation type in in that mode, the associated variable is free before that application and bound after it.
  • For every parameter that has instantiation type out in that mode, the associated variable is bound both before and after that application.
• For each not operator (and more generally, in negative context):
  • Every variable mentioned outside the scope of the not has the same instantiation before and after the not.

Which ordering to use is not predetermined, but the modes of predicate applications in it are predetermined in order to avoid ambiguity, so that we can't instantiate in two different ways, which would risk getting two different results.

This is a fairly blocky way of treating modes and I expect it will be treated in a more fine-grained way later.

What definitions are

In some systems, definitions are really axioms in disguise. In Trade Logic, that would be an intolerable hole; bettors would quick learn to exploit it and ruin the system. So we won't go in that direction.

Our definitions will expand names to parameterized formulas. That is, each definition will map a unique identifier to:

• A formula
• A parameter list: A non-repeating list of variables.
• A set of modes, all legal for that formula with respect to the parameter list.

A definition is used in a formula by giving its name and an argument list of the correct arity in a position where a (sub)formula can appear.

So a definition:

• is a predicate, not a function. It "returns" a fuzzy boolean, not an object.
• is not a clause. Unlearn your Prolog for this. A name has one definition, you don't add more clauses later.
• is total. Its argument list accepts any type of object.
• is used in some particular instantiation mode.

I don't think we need to require that definitions be in a Tarski hierarchy. I expext Trade Logic to be exposed to many other sources of unclarity besides self-reference. Undecideable issues won't ruin the system. However, we may need to use a Tarski hierarchy for decision markets, which want controlled language and decideable issues.

Selection operations

Selection operations are also predicates. They are used the same way as definitions.

I presuppose a set of primitive selection operations. But that's beyond the scope of what I'm talking about right now.

For purposes of issue decomposition, any primitive selection operation that cannot be satisfied behaves as though it trades at $0 (ie, its yes trades at $0). For instance, "Select a living dodo bird". A selection operation that is satisfied behaves as though it trades at $1.

What a wff is

Having said all that, now I can recursively define a well-formed formula (wff) in Trade Logic as:

• One of the built-in operations applied to the proper number of wffs:
  • The unary operation (not) applied to a single wff.
  • One of the binary operations applied to two wffs.
• A predicate application, consisting of:
  • The name of a predicate
  • A list of variables whose length matches that predicate's arity
  • A mode of that predicate

Which formulas are the same?

Trade Logic does implication by assembling the conclusion from parts of the premise(s). So we want to know when two formulas are the same.

Two formulas represent the same issue (and decomposition) just if they are structurally the same, except allowing arbitrary permutations under and and or.

In other words, put subformulas under and or or into some canonical order before comparing formulas. Then mostly ignore the variables, except that the same respective variables have to appear in the same respective positions.

Footnotes:

¹ Back then he called it idea futures.