Tehom: Mutability And Signals

Mutability and Signals

Recently I've been working on Rosegarden, the music sequencer. It uses Qt which uses signals.

Signals implement the Observer pattern, where an object notifies "observers" via signals. A signal is connected to one or more "slots" in other objects. The slots are basically normal methods, except they return nothing (void). When a signal is emitted, Qt arranges for the slots to be called, other than those of deleted objects. So far, I find it works easily and elegantly.

This made me wonder: Could signals take the place of mutability in Scheme? And might that give us both referential transparency and reactiveness simultaneously?

There's not much support for signals for Lisp and Scheme. There's Cells, but it seemed to be conceived of as just a super-spreadsheet. I want to go much further and use signals to re-imagine the basics of object mutation.

Quasi-mutation: The general idea

Basically, we'd use signals between constant objects to fake mutability.

Objects can't mutate.

"Slots" are closures.
- Closures would typically know a target object. Possibly as environment as record.
Signals are emitted with respect to particular objects.
- Not "by objects". Again, we're not object-oriented. We're just indexing on objects.
- Ability to emit is controlled by access to objects and signal types.
- Indexing on one particular argument seems overly special, so I contemplate indexing on any relevant arguments. This is again similar to generic functions.
Signals can be connected to slots.
- The signals go to where the object's respective signal is connected. They are indexed on objects.
Constructors connect the signal replaced from the parts to the constructed object.
- More precisely, to a closure that knows the object.
- The closure would fully represent the objects' relation. For instance, mutable pairs might have the slots new-car and new-cdr with the obvious meanings.
- But not for immutable objects. Immutable objects' slots would not be new-car and new-cdr, they would raise error.
- The constructed object can access its part objects, in appropriate ways by its own lights. For instance, a pair object could retrieve its car and cdr objects.
- This particular signal replaced is not exposed.
- The details of replaced will be refined below.
Slots such as new-car will typically:
- Construct a near-copy of the object, with the new part in the old part's place. This effectively connects a new version of the object to the new part and disconnects it from the old part.
- Emit replaced with respect to the object, propagating the change.
"Normal" setters such as set-car! emit replaced wrt the old object with the new object as value.
- That's just the classical way. There's plenty of room to do clever new things with signals.
- As above, doing this to immutable objects causes error.
Constructed objects behaving this way would include at least:
- Mutable pairs (and therefore mutable lists and trees)
- Environments
- Continuations. While not often considered object-like, continuations have parts such as the current environment and their parent continuations.
External-world-ish objects such as ports react to signals in their own appropriate way, not neccessarily propagating them further.

As if

Literally implementing ever pair with at least two signals between itself and its car and cdr seems prohibitive if not impossible. Physically, it couldn't be the only mechanism of mutation. So I'm talking about a mechanism that acts as if it's continuous down to basics like pairs and lists, but really uses a more modest mechanism where it can (presumably containment, as now).

Circularity

My blog readers, being smart, will already be wondering what happens when replaced is propagated in a circular structure. Does it propagate forever, crashing the interpreter? That might go something like this: The signal propagates from pair to pair, repeatedly reaching its original location, pointlessly representing more new objects that differ only from the k*N nth cdr, and never finishing because there's always an (k+1)*N nth cdr to represent.

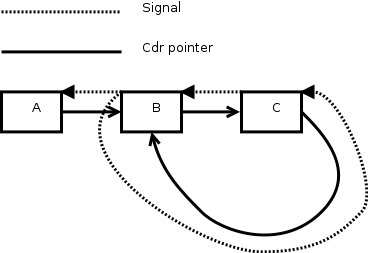
For instance, in the circular list above, suppose we gave object C a new value. It emits (replaced New-C C), which B receives in new-cdr. B emits (replaced New-B C) which both A and old C receive. Leaving aside A's reaction, old C then emits (replaced New-Old-C C) which old B again receives. A is going to be deluged with infinite signals, and we will keep making new copies of old B and old C. Worse, we make many new-Bs when we only have a place for one.

The too-easy answer would be to block all repetitions between the same two objects. That fails, because we re-emit on new copies. So also block repetitions where the objects are the same except that one is replaced by an updated copy?

So as a first draft, I propose that these built-in signal emissions:

Be each associated with a unique ID
Refuse to propagate that ID circularly

The ID would be an opaque ID equal? only to itself. It would be unique to a given cascade of emissions. That is, set-car! etc would make fresh IDs but new=car etc would use the ID of the replaced signal that provoked it.

One subtle point: It suffices for the signalled object itself to recognize repititions. Originally I thought repititions would have to be recognized across a transitive closure. But only the original object is connected to by its contents, and connections from new parts to new object don't receive any signal to propagate.

What about structural information?

The above is progress, but it discards structural information.

Consider an application that displays the first N items from a possibly-circular list on screen, and redisplays them just as needed (Say they are formatted in some time-consuming way and different screen locations can't share this work) The display would want to be notified of all the nth cdr occurences of a changed element. The approach above wouldn't permit that.

So when there's circularity, let's switch tactics and use polling to retrieve information as needed. Let any circular object provide a stream of all the replacements that occured in it for a given emission-ID. Applications only read the stream as far as they need to and the rest is not really generated.

But often a slot would prefer to get a simple new object, without replaying all the detailed changes.

Desiderata

To sum up the desiderata on this:

We want slots to be able to replay detailed changes.
We want slots to be able to just get a new object
We don't want mutated objects to have to guess what their target slots want, which may not even be the same for different slots.
We don't want mutated objects to have to do inordinate (even infinite) work preparing these signals.
We don't want to make assumptions about the topology of the mutated object. It can be an arbitrary directed graph.

A thought-experiment sequence of operations

The sequence of operations on the circular list above would go something like this. Here I use FOO.N to indicate the nth version of FOO.

We gave object C.1 a new car, V (we emit replaced.1 to it) Its change is:
- "Replace car with object V". We'll represent this as
  - The trivial accessor identity.
  - A promise to construct V (Trivial since we started off knowing it)
replaced.1 reaches C
We emit replaced.2 for C. Its change is:
- A disjunction (or) of
  - "Replace what you're holding with C.2"
    - identity
    - A promise to construct C.2
  - "Replace car of it with V"
    - car
    - Promise of V
replaced.2 reaches B
We emit replaced.3 for B.1. Its change is:
- A disjunction (or) of
  - "Replace this with B.2"
    - identity
    - A promise to construct B.2
  - A disjunction (or) of
    - "Replace cdr of this with C.2"
      - cdr
      - A promise to construct C.2
    - "Replace cddr of this with V"
      - cadr
      - Promise of V
replaced.3 reaches A.1
- We'll say the promises are not forced yet. If they are, that still forces these following operations to occur first.
replaced.3 also reaches C.1. Here we encounter a repitition. C.1 has already encountered a signal from this trigger. We don't want to emit another consequence of it to the same places. Instead we want to fold the signals together.

Let's stop operations and look at it

If we made replaced.4, its change would be:
- A disjunction (or) of
  - "Replace this with C.2"
    - identity
    - A promise to construct C.2
  - A disjunction (or) of
    - "Replace cdr with B.2"
      - cdr
      - A promise to construct B.2
    - A disjunction (or) of
      - "Replace cddr of this with C.2"
        
        cddr
        
        Again, a promise to construct C.2
      - "Replace cadr of this with V"
        
        caddr
        
        Promise of V

So replaced.4 resembles replaced.2. The big change is that instead of "Replace car of this with V", we have a cdr replacement. It pushes "replace with V" down to another cycle of the loop. That doesn't support the "display circular list" example, which was our motivation for doing this. So:

We need to support something that can mention both the car replacement and the cdr replacement of C.1
We need to effectively be able to adjust previous signals instead of emitting more.

I first considered and discarded an approach of rewriting the second disjunct into a conjunction.

Now the most tempting approach is to rethink the car replacement operation. It did not fully describe the object, it just described the new car, V.

Let's say that all such operations are in fact constructors, and in the case of "Replace car of it with V", we let the cdr argument default to the current cdr.

Timing issues:

The default can't be committed to until the signal and its consequents have stopped propagating.
We know this by Emission-Id.
So forcing one of these promises first causes the signal to propagate until it's done.

This sounds quite like what I would expect from a solution. Constructors "stand for" the objects they make, as is often the case in RT languages. We are getting a structure that's isomorphic to the original object (circular list of period 2). "Just mutate contents" remains a valid optimization as long as we're in a closed system (And a tempting one; I have to keep reminding myself that we're conceptually replacing mutation with signals so it won't do)

The new structure of replacement info

So replaced.2's replacement info actually looks like:

A disjunction (or) of
- "Replace what you're holding with C.2"
  - identity
  - A promise to construct C.2
- "Construct it with V as car"
  - Arguments
    - car : Promise of V
    - cdr : C.2's cdr value, defaulting to C.1's cdr value.

Default arguments

The action of replaced.3 on C.1 just provides a value for the cdr argument. Re-emission is not needed, nor wanted since at C's cdr the signal has reached a join.

So the default cdr argument is held in a sort of limbo until it's given or not. That's a lot like mutation in itself. So it too is managed by signals:

"All done". Signal has fully propagated, use defaults for anything not filled.
"Use this" Accessor Value. After receiving "use this", "All done" has no effect.

These are of course quasi-mutating the stream argument of replace. There's an infinite regress there, but since it is all behind promises that delay evaluation until after this is done, I think we can consider it as if the stream had had one unchanging value forever.

Structure of the change stream

So each "cell" of the stream of operations changes consists of a disjunction on constructors and values, rather than a cons cell. Each disjunct can be:

A promise of a value
A promise of a constructor parameterized by promises of values

So it's like an n-ary tree-stream.

Note that this naturally orders the change stream from shallow to deep. If it was ordered from deep to shallow we couldn't find elements in finite time.

This doesn't preclude specialized representations that (say) compact multiple simple cdr accesses to an nthcdr access. These could be represented as additional constructors in the disjunct.

Object identity

Above, I said "constructed object can access a part object", not "a part's value". Since objects no longer ever change value, the difference is subtle. It's just this: the object has a single set of signal connections. So it has a single identity. So there is a trace of object identity remaining.

One could represent identity value-wise by saying that values consist of a (classical) value and an "object-identity" value, and that object-identity values are opaque and unique except as shared by this mechanism. So signals are connected with respect to object-identity values.

It has a flavor of "the long way around", but it lets us treat objects entirely as values.

Object versioning

Different versions of an object have different Object-IDs. Imperatively this wouldn't be anything, since two simultaneous references to the same object can't have different values. But here, one can both mutate an object as far the the world is concerned and hold onto its old value. But it should never be the case that objects are eq? but not equal?. So different versions have different Object-IDs.

The equality predicates

Equality:

equal?

is what it normally is in Scheme or Kernel: The objects have the same current value.

eq?

A and B are eq? just if

(equal? identity-of-a identity-of-b)

=?

is just an optimization of equal?

Signals and immutability

I mentioned that I was thinking about immutability in regard to this. So far, I've just described how to duplicate mutability with signals.

For immutable objects, some or all slots would still get connections, but would raise error instead of propagating mutation.

But that's only half of the control we should have over mutation. We'd also like to guarantee that certain evaluations don't mutate even mutable objects they have access to, eg their arguments, the environment, and dynamic variables. The "foo!" convention indicates this (negatively) but doesn't enforce anything. "foo!" convention notwithstanding, we'd like to guarantee this from outside an arbitrary call, not from inside trusted combiners.

Blocking signals

So we'd like to sometimes block signals. If signals were emitted anyways, they'd be errors and would not reach their destinations. So if replaced is blocked, code either doesn't try to mutate objects or tries and raises an error. Either is consistent with immutability.

ISTM the simplest way to block signals is to disconnect their existing connections and connect them to error combiners. When the call is done, restore their original connections. However, that doesn't play well with asynchrous execution.

Instead, we'll make a copy of the original object that will (probably lazily) infect its parts with "don't mutate me in this scope".

Scope

For a traditional imperative language, where flow of control and scope are structurally the same, we could block signals in specific scopes, recursively. But for Scheme and Kernel, that won't suffice. What would happen if an object is passed to a continuation and mutated there? We've broken the guarantee that the object wouldn't be mutated. Any time we let objects be passed abnormally, this can happen.

We might try to:

raise error if affected objects are passed to continuation applications, or
"infect" the other scope with the signal restrictions.

Neither is appealing. In this mechanism, continuing normally is also passing to a less restrictive scope. And continuing normally should behave about the same way as continuing abnormally to the same destination. We also don't want error returns to permanently "freeze" objects.

So ISTM we must distinguish between continuing to a (not neccessarily proper) parent of the restricting scope (normally or otherwise) and continuing elsewhere. Signal blocks are removed just if control reaches a parent. This is essentially how Kernel guards reckon continuation parentage.

Doing this for all object parts

We'd usually want to say that no part of any argument to a combiner can be mutated. It's easy enough to treat signal connections from the root argobject. But we need to "infect" the whole object with immutability, and not infect local objects, which may well be temporary and legitimately mutable.

Since these arguments are ultimately derived from the root argobject, what we can do is arrange for accessors to give immutable objects in their turn. But they have to be only temporarily immutable - blocked, as we said above. And we'd prefer to manage it lazily.

So I propose that accessing a blocked object gives only objects:

whose replaced signals are re-routed to error, as above, until control "escapes normally" (an improper parent continuation is reached)
which are in turn blocked, meaning they have the same property infecting all of their accessors.

Non-pair containers

Non-pair containers are not treated by mechanisms like copy-es-immutable. But we want to treat immutably fully, so they have to be treated too. This is the case even for:

Environments
Encapsulation types. In this case, their sole accessor is required to do this, as all accessors are.
Ports. Administrative state or not, they can be immutable.
Closures. Anything they return is considered accessed and automatically gets this blockingness. Their internal parts (static environment, etc) need not be blocked.
Continuations. Like closures, what they return is considered accessed and automatically gets this blockingness.

Exemptions

We'd like to be able to exempt particular objects from this. Some combiners mutate an argument but shouldn't mutate anything else. There'd probably be a signal-block spec that would specify this.

Blocking signals to keyed dynamic objects

We can easily extend the above to deal with dynamic environment, but keyed dynamic objects are not so simple. Their accessors would be covered by the above if derived from the argobject or the dynamic environment, but they need not be.

So we need an additional rule: Keyed dynamic objects are blocked if accessed in the dynamic scope of the blocking. That's recursive like other blockings. Keyed rebindings in the dynamic scope aren't, because one might bind a temporary that's legitimately mutable.

Side note: I'd like to see a stylistic convention to differentiate between combiners that mutate their arguments ("foo!") and combiners that mutate something else, meaning either their dynamic environment or a dynamic variable (Say "foo!!")

Interface to be defined

I've already written a lot, so I'll leave this part as just a sketch. To support all this, we need to define an interface.

A means of defining new signal types
- Returns a signal emitter
- Returns a signal identifier for `connect' to use.
A signal scheduler. By general principles, the user should be able to use his own, at least for exposed signals. It's not too hard to write one with closures and continuations.
Means for the user to emit signals
Means for the user to connect and disconnect signals
- Not exposed for many built-in objects such as pairs.
- "capture all current", as for blocking
- "disconnect all"
block-all-signals: connects all signals to error continuation
- Possible argument `except'
(Maybe) block-signal: connects given signal to error continuation
A "dirty-flag" mechanism, often useful with signals.
Possibly a priority mechanism.

Some possibilities this raises

Use the signal scheduling mechanism for managing constraints. Since when we can enforce immutability, constraints become very tempting.
Provide general signals
Provide an interface to Lone-COWs, a sort of copy-on-write object optimized for usually being uniquely referenced/owned.
Supplying "out-of-band" signals to a debugger or similar. They really do need to be out-of-band.
Provide a broadly applicable interface for redo/undo. It could basically just capture historical copies of objects.

Glorified footnote: Aren't signals a lot like callbacks?

Somewhat. The differences are:

Signals are N to 1.
Signals are associated to some sort of signal-type object. One creates a signal of a specific type. In Qt, this is specified as "signal:" members of a class.
Signals are scheduled more freely.
Signals to "dead" objects do nothing. Their existence doesn't keep objects alive; in this they are like weak references.
The sending object does not explicitly track its observers,